Algoritmos computacionales: Maquinas de Turing

Una máquina de Turing consiste, básicamente, en una cinta infinita, dividida en casillas. Sobre esta cinta hay un dispositivo capaz de desplazarse a lo largo de ella a razón de una casilla cada vez. Este dispositivo cuenta con un cabezal capaz de leer un símbolo escrito en la cinta, o de borrar el existente e imprimir uno nuevo en su lugar. Por último, contiene además un registro capaz de almacenar un estado cualquiera, el cual viene definido por un símbolo. Los símbolos que definen el estado del dispositivo no tienen por que coincidir con los símbolos que se pueden leer o escribir en la cinta. En los programas presentados en el artículo, los posibles símbolos a leer o escribir en la cinta son el 0 y el 1, y los posibles estados se representan con letras mayúsculas. En el emulador, existe un cambio en la representación del estado, usando para ello los números del 0 al 99, para permitir un mayor número de ellos.

La máquina tiene un funcionamiento totalmente mecánico y secuencial. Lo que hace es leer el símbolo que hay en la casilla que tiene debajo. Después toma el símbolo del estado en que se encuentra. Con estos dos datos accede a una tabla, en la cual lee el símbolo que debe escribir en la cinta, el nuevo estado al que debe pasar y si debe desplazarse a la casilla izquierda o derecha.

Descripcion de la maquina de Turing.

La idea de la maquina funcion con un Cabeza de Lectura y Escritura que lee una cinta infinita.

Cada vez que lee, borrar el contenido anterior, escribe un nuevo contenido, para luego Avanzar un lugar hacia la izquierda o Derecha.

Con esta maquina se puede realizar cualquier computo de las maquinas computadoras actuales

La maquina de Turing puede considerarse un automata capaz de leer lenguajes formales (es un conjunto de palabras (Palabras son cadenas de caracteres) de longitud finita que se forman a partir de un alfabeto (_Conjunto de caracteres) finito.

Definicion de una maquina de Turing de una sola cinta :una 6- tupla $M=(Q, \Gamma, s, b, F, \delta)\,$ ,

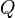$Q \,$ es un conjunto finito de estados.
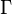$\Gamma \,$ El alafabeto de la cinta, un conjunto finito de símbolos de cinta
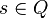$s \in Q$ Estado Incial.
$b \in \Gamma$ Ssímbolo denominado blanco.
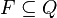$F \subseteq Q$ es el conjunto de estados finales de aceptación.
$\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}\,$ función de transición, donde L es un movimiento a la izquierda y R es el movimiento a la derecha.